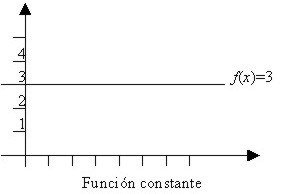
Función constante
Decimos que una función f pertenece
a la familia de las funciones
constantes si se puede expresar analíticamente de la
forma:
f(x)=k, siendo k un
número real
Su representación gráfica, como ya
sabemos, se corresponde con una recta paralela al eje X.
Como observaremos, a lo largo del
desarrollo de esta unidad basta con representar una función de esa familia, a la
que llamaremos función base, para,
mediante transformaciones en el plano (la mayor parte movimientos), obtener la
gráfica de cualquier otra función de esa familia.
En matemática se llama función constante a aquella función matemática que toma el mismo valor para cualquier valor de la variable. Se la representa de la forma:[1]
Funciones reales de una variable real
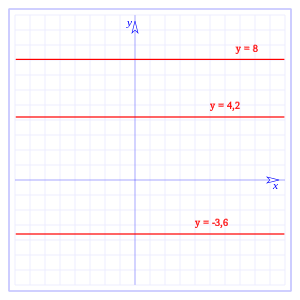
Como se puede ver es una recta horizontal en el plano cartesiano, en la gráfica la hemos representado en el plano, pero, como se puede ver la función no depende de x, si hacemos:
La función constante como un polinomio en x
Si un polinomio general, que tiene la forma:
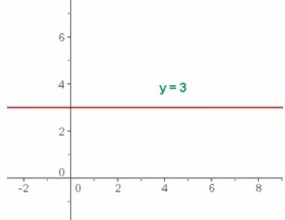
Una función de la forma f(x) = b, donde b es una constante, se conoce como una función constante.
Por ejemplo, f(x) = 3, (que corresponde al valor de y) donde el dominio es el conjunto de los números reales y el recorrido es {3}, por tanto y = 3. La gráfica de abajo muestra que es una recta horizontal.
Funciones reales de una variable real
Como se puede ver es una recta horizontal en el plano cartesiano, en la gráfica la hemos representado en el plano, pero, como se puede ver la función no depende de x, si hacemos:
La función constante como un polinomio en x
Si un polinomio general, que tiene la forma:
Una función de la forma f(x) = b, donde b es una constante, se conoce como una función constante.
Por ejemplo, f(x) = 3, (que corresponde al valor de y) donde el dominio es el conjunto de los números reales y el recorrido es {3}, por tanto y = 3. La gráfica de abajo muestra que es una recta horizontal.
 |  |


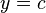



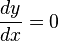
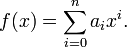
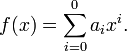

No hay comentarios:
Publicar un comentario